1. Introduction

Our study was postwar motivated by the existence of Cybernetics (Wiener, 1961; Ashby, 1956; Ashby, 1960) in disciplinary academics. Certainly, the world of Cybernetic is unique, universal, and attractive. However, this theory is not directly applicable to the practical treatment of (discrete/digital) Industrial engineering (IE) & Operations research (OR) of huMan, material/machine, money/monetary, and Information (3M&I). Thus, there are some conflict stages and a long way to the art of digitalization at body science and realization.

Based on Wiener’s work (Wiener, 1961), we have been observing object shifts and advances in animal, machine, and information. Thirty years ago, Nof et al. (2015) presented the PRISM concept, which includes production, robotics, and integration software for manufacturing and management, and established the PRISM Center at Purdue University. Conversely, the 3M&I concept and its art was previously named by the author based on the definition of industrial engineering (IE) in 1948.

Although the value (energy) concept is not positively seen under the PRISM or Cybernetics categories, it would still be critical in the modern closed-earth versus smart-world age and toward the art of 3M&I diversity. Classical Cybernetics would also be critical at the black-box and feedback scheme and desirable to the white-box (pair-matrix) and look-forward (ahead) scheme toward post-Cybernetics.

Since 1967, steady progress on the 3M&I concept has been made in fields of factory physics, management, and queueing systems with losses (Matsui, 2016). This has led to the abyss predicted by Matsui’s equation (dualism) and the formation of a pair map (rotational phase) at the point corresponding to the maximum profit from the collaborating manufacturing and sales centers (Matsui, 2002). The problem of profit maximization (W) is similar to that of the collaboration of sales (Z) and lead time (L) in Matsui’s equation: W = ZL, and is probably reaching to the concept of ternary SW/pair-map at the central dualism of body.

Early research on this topic and progressive physics was motivated by the queueing theory and inventory. Matsui’s equation was obtained in 1977, look-ahead logics became available, and has recently gained attention as a universal principle that can be described mathematically via algebra, geometry, analysis, and probabilistic control. Matsui’s equation (discrete type) is similar to or has a dualism analogy with Newton’s law (analog type) in the interdisciplinary problems of physics and economics. See Figure 1.

At the beginning of this body’s central dualism, the pair map was first invented from a cooperative game, and characterized later by the microcosm of cross-ellipse images in a matrix of input–output pairs. In algebra, the field theory helps solve the pair matrix in an input–output system, and the ellipse map clarifies the economics of the invisible collaborations between bodies.

Currently, questions are being raised regarding the relationship between nature and “artifact bodies,” also known as 3M&I bodies. The academic and original nature of the central dualism (Matsui, 2002, 2016) in this topic is a product of developmental research that　has yielded middle-phase pioneering results and pair maps. This middle-phase mechanism represents an artificial computer architecture problem, and its boundary (interface) in recent cyber–physical systems remain unresolved.

Pair maps (Matsui, 2002, 2008, 2013) manifest this middle problem in supply and demand systems. They appear to be two-dimensional representations but are, in fact, three-dimensional miniaturized models (microcosms) of artifact bodies and are fundamentally governed by the dynamism of Matsui’s equation (Matsui, 2002, 2016) . Recently, this was elaborated in (Matsui, 2020).

In addition, in numerous fields ranging from economics to physics, lower micro and higher macro relationships do not emerge in visible forms. Thus, their boundaries and connecting relationships are overlooked. Matsui’s equation represents a dual connection, offering a bridge to fields of physics, together with signposts (Matsui, 2013, 2020) and economics via interindustry relations entailing table connections and the future information society.

To unravel this middle phase, we must focus on realizing corporate robots (Matsui and Ishii, 2019; Matsui et al, 2021) as the embodiment of pair maps at an industrial design stage. This task concerns human existence and corporate middle management and focuses on the nature of the essential scientific role of middle managers.

Important research values that are crucial to the primal state of being (Sein) and ideal human society (Sollen) are those that lead to the development of theories and methodologies for management approaches, emphasizing a middle phase that is neither at the top or bottom (Matsui, 2002, 2008, 2016; Matsui and Fujikawa, 2005). These values contribute to the high and efficient management of the world of artifact bodies and promote sustainability.

With regard to post-cybernetics, the repetitive and cyclic processes of nature versus artifact bodies with delay/loss can be formulated as shown in Figure 1 by considering the profit equation (cyber/macro level) and progressive equation (physical/micro level) (Matsui, 2008, 2016). The process can be verified based on Sein, central dualism, ternary SW and chameleon’s criteria at the physical body.

2. Pair-Map Duality and Matching

2.1. Pair-Map Duality and Mismatching Problems
Herein, consider a 3M&I body as a system consisting of inputs and outputs (with a goal). This system has functions that maximize the output and minimize the input. Furthermore, a two-term input–output matrix (Matsui, 2008), referred to as a pair matrix, is considered a collaboration function for the input and output.

Each element of this matrix is a paired element (output gain and input loss). In examples of nature or artifact bodies, various graphic patterns are seen in the pair matrix, though they are all characterized by intersecting ellipses. Thus, an elliptical rotation mechanism generally referred to as a pair map (generic name) is observed Matsui, 2002, 2008, 2016; Matsui and Fujikawa, 2005).

Consider the interconnections between manufacturing (input) and sales (output); the aforementioned intersecting ellipses have intersecting axes, one of which (corresponding to positive correlation) is referred to as economic efficiency, and the other (corresponding to negative correlation) as reliability. The intersection point of these fundamentally contrasting axes represents an individual objective (profit maximization) that reaches an equilibrium balance (win–win or mutation point). A variant of a hyperbolic type is seen in this case, which has an orbit toward the center.

Economic efficiency and reliability represent the gain and duration of individual systems, respectively. Here, system duration negatively correlates with gain, implying that gain size is related to redundancy within the required time. Thus, no redundancy is present for large gains; if substantial redundancy is present, the gain decreases, increasing the loss and reducing profit.

Furthermore, various forms of map diversity are observed; by discovering the possibility that they may provide a universal bird’s-eye view (microcosm) of artifact bodies and their clock dynamism, we proceed to verify and comprehend them, thereby proposing various forms and ideal shapes for artifact bodies.

2.2. Body Universal Law of Nature Versus Artifact Bodies
The diversity in form is believed to originate from the duality (Matsui, 2013, 2016) in numerical and monetary (value) equations corresponding to Matsui’s law, similar to the duality in motion and power (energy) equations in Newton’s laws. The duality of matching and mismatching (skewness) in this middle phase arises in various phenomena related to the relationship between nature and artifact bodies, as listed in Table 1.

Table 1. Cycle duality: nature versus artifact bodies

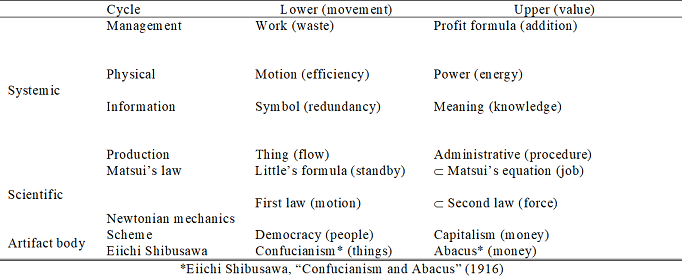
Matsui’s equation (W=Z×L) is a universal law (Matsui et al., 1978; Matsui, 2005a) derived by Matsui for artifact bodies, where Z denotes the cycle time (cycle), W is the waiting time (value), and L is the number of people waiting (quantity).

The multiplication used in this equation is not a simple product but a dynamic adjustment mechanism (role) for reaching equilibrium. For example, typical physics laws (concept of leverage) and economics (concept of specific gravity) are formulated in a vector space with Matsui’s law as their basis.

Science has advanced by discovering patterns of regularity (cycles) because cyclic phenomena are always considered reproducible and provable. This cycle (Z) is a summation of Z = regular thing (X) + irregular thing (D).

The latter results from the interaction with the surroundings and is generally regarded as a delay phenomenon (e.g., reacting, waiting, waste, overflow, margin, error, or profit). Studies on the laws governing this interaction are relatively new. However, a linear relationship exists between delays and overflows in systems (Matsui et al., 1978; Matsui, 2005a) and constraints under which cycles stop mid-way (Matsui, 2005b; Yamamoto et al., 2006),  as in the CSPS model (Reis, 1967).

For artifact bodies, L=λW (Little’s formula, where λ denotes the arrival rate) represents the starting point of a queue, and equations such Matsui’s law, i.e., W=ZL, are later derived for the loss-allowed system. For physical bodies and electromagnetic systems, Newton’s first formulation of dynamical systems and Joule’s law can be considered, respectively. See Figure 1.

These laws have all been shown to be essentially isomorphic (Matsui, 2011, 2016). Generally, Matsui’s law holds mathematically (algebraically, geometrically, analytically, and stochastically) in nature versus artifact bodies. Moreover, the concept of energy in a physical body corresponds to that of money (value) in an artifact body (similarity).

3. Nature Versus Artifact Bodies and Formulation

3.1 Ideal Form and CSPS Model
A nature versus artifact pair body (Ordered-entry, OE, type) was found in (Matsui, 2016), and the pull-type in the merge processes (r+v→ λ) is believed to be a typical ideal form thereof. Figure 2 refers to the Diet–Absorption–Energy (DAEn) of Ternary SW (sandwich), which resembles the Eastern “danshari” (“refuse–throw away–separate”) style. The problems with the ideal form in Figure 2 are duality matching, mismatching, and skewness.

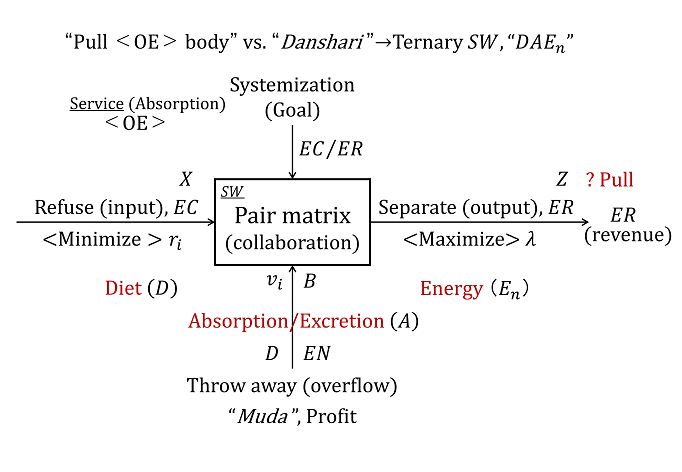
From a separation process study (λ → r + v) of the CSPS model (Matsui, 1978, 2005a), the relationship between delays E (D) and E (η) of a pair-body (push AL/OE type) can be seen in Figure 3. Here, when ρ < 1, the foreseeable chameleon criterion is as follows.

For arrival λ, based on service X and buffer C=1: 0.7: 0.7 (1), X: D=0.6: 0.4, and upper chameleon criterion (medium) (Matsui, 1978, 2013) of 0.6 versus 0.4 is simultaneously satisfied.

In addition, when ρ=1 , under a Poisson arrival, X: D=2: 1, and a chameleon criterion of 0.6 versus 0.4 is obtained. Furthermore, in a heat efficiency model, a dual AL-type pair body can be determined.

Moreover, the first case of the merge process ischanged to r (X) = λ– v (D), and in DAEn, a better diet (X) would lead to better absorption (D). Note that this fact in the value type would introduce the opposite criteria.

3.2. Formulation of Nature Versus Artifact Bodies
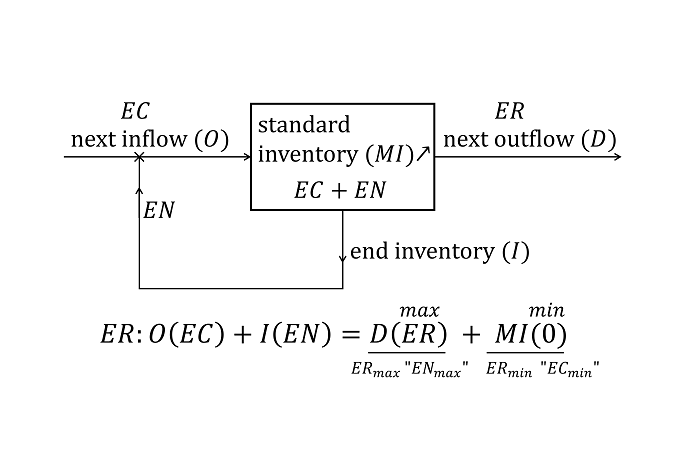
From Figure 2, the nature versus artifact bodies can be expanded to the cyber–physical body, and formulated by considering the profit equation (cyber level): ER = EN + EC in Section 3.1, and progressive equation (physical level) in cyclic processes:

Then, the logical formulation of bodies is seen at Figure 4.  According to Figure 4, the formulation implies that the goal approaches the state variable of the standard inventory (MI) to the next outflow (ER). The standard inventory is regarded as a control variable that maximizes the marginal profit. This could be reduced to a formulization problem using the Matsui’s matrix equation (Matsui’s ME) (Matsui, 2018), which partially agrees with a Chinese theory (ki-sho-ten-ketsu logic).

Matsui’s ME is a logical matrix product, i.e., (Introduction × Development × Transformation × Conclusion × Balance) = Goal. The type II Matsui’s ME is similar to the Ricatti equation in control theory (Bittanti, 1991).

Results should be presented precisely and should not contain material that is appropriate in the discussion. Units, quantities, and formulas should be expressed according to the International System (SI units). All measurements should be given in metric units.

4. Physical Body Duality (dualism) and Mismatching

4.1. Physical body cycle and pair-map expansion
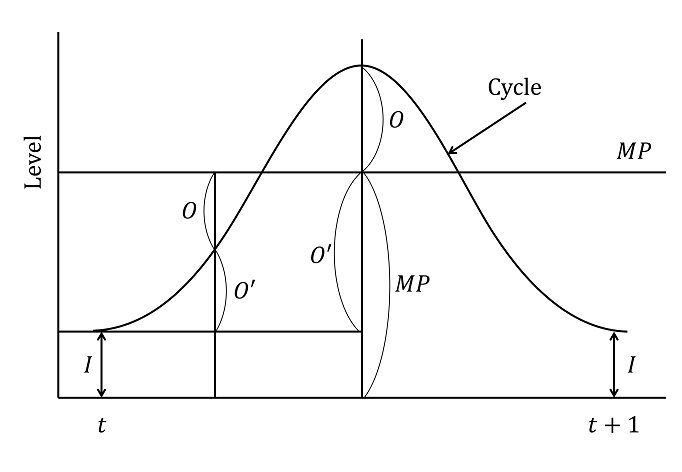
For physical body cycles, the following progressive equation (flow control formula) is generally returned, and it is similar to the wave equation of the discrete type (1). The lifecycle (rotating system) of a physical body according to the flow control equation is depicted in Figure 5. This is a wave equation of the discrete type. Then, our pair map of a physical body can be expanded to accompany the rotation cycle in Figure 6.

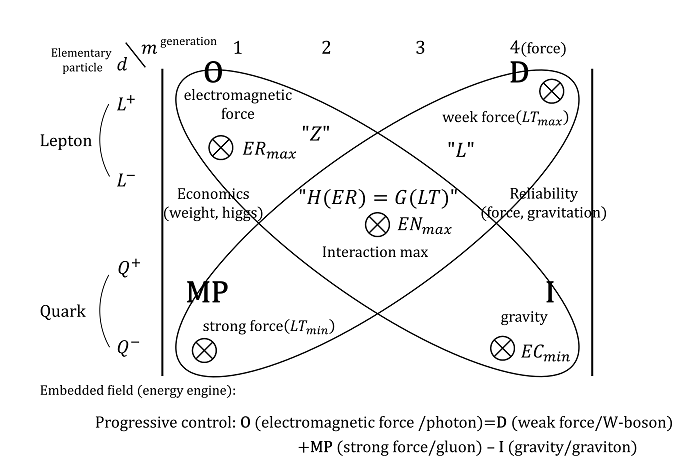
As shown in Figure 7, the chameleon criteria (Matsui, 2011) introduced in the discussion of duality mismatching correspond to the media. These criteria are based on the linear equations for delays and overflows (Matsui et al., 1978; Matsui, 2005a)

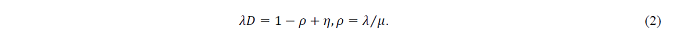
The design criteria of CSPS artifact bodies satisfying this relationship is known as conditional expressions (chameleon criterion), given by the following equation:

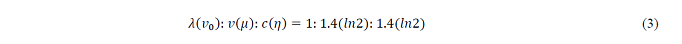
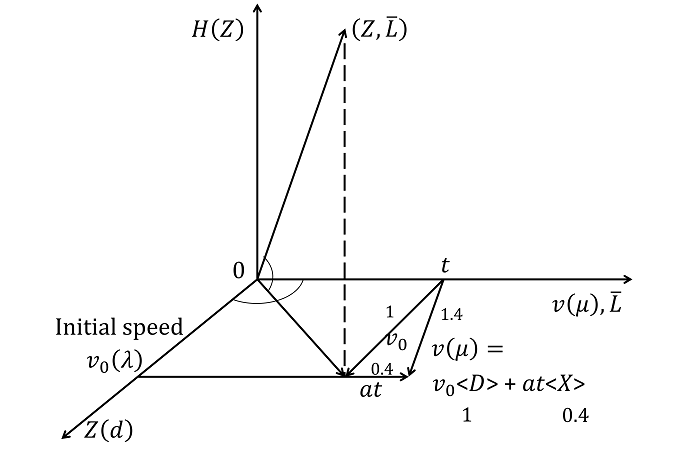
This problem in physical bodies can be seen in Figure 7, where λ corresponds to the initial velocity v, service rate v corresponds to velocity v, and c corresponds to acceleration a (Walker, 2001). In addition, from a duality perspective, earnings ER corresponds to energy (Hamiltonian), and lead time L corresponds to motion p (= v L ).

4.2. Economic Efficiency Versus Reliability in Physical Body
Here, Figure 7 is an expansion of the pair map for a physical body provided in Matsui, 2002; Matsui and Fujikawa 2005). The relationship of economic efficiency (energy) versus reliability (gravitational pull) is further clarified. In general, the artifact body (money) is a Hamiltonian (energy) of a physical body.

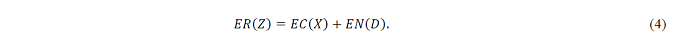
Moreover, EC(X) is equal to the motion energy (mv/2). When X→Z(=X+D), the following equations hold:

In particular, when 1=λ=μ, D=η,and D=X=1, then

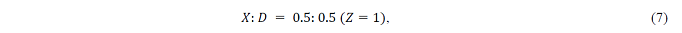
where λ and μ are different ( λ: μ=1:1.4), and X: D=0.6:0.4.

In addition, for reliability (gravitational pull), if G is the gravitational constant, then

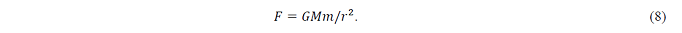
Here, if we consider GM/r→Z(d),m/r→L, then the gravitational force matches the lead time.

On the other hand, the Hamilton (4) could be represented at the ternary SW in Section 3.1 and Figure 5 as follows: EC(X)+EC(D)→ER(Z).  Also, some relaxation problem of ternary SW with allowance (buffer) is geometrically seen at the progressive equation (1), Figure 6., and could be simultaneously displayed by 3D-like pair-map at Figure 7. Probably, this would result in the advanced field theory with ternary and pair-map at the central dynamism of body.

5. Pair maps and black holes

5.1. Artifact Body Wave Motion Equation and Conical Surfaces
Recently, the wave motion equation for the clock system of artifacts body type was obtained from a pair-map three-dimensional polar display (θ,∅) (Matsui, 2018). From this, the conical surface in Figure 8 was obtained at the center of the pair map. From the geometric relationship in (9) (Matsui, 2018), we derive (10) based on a trigonometric theorem.

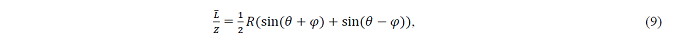
Then, we assume θ^+ =θ+φ and θ^– =θ-φ, which implies that

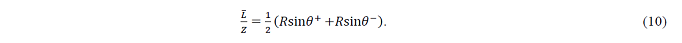
Furthermore, if u→y, then x,y are as follows:

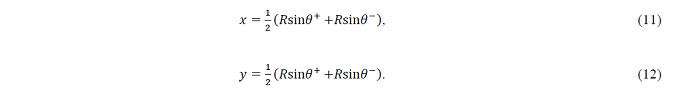
Here, (2) is as follows:

From the above, x^2+y^2=R^2 cos^2⁡φ, and from d=cos⁡φ,

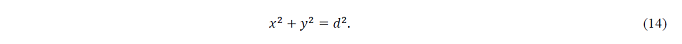
Therefore, point M(x,y) is on a circumference of a circle of diameter d centered at the origin, and the value of y is the y coordinate value at this time. In addition, because 0<d<R, according to (5), d is a function of x,y and d=√(x^2+y^2), we express a conical surface in three dimensions (x,y,d), as shown in Figure 8.

5.2. Artificial black holes versus Chameleon’s criteria
Normally, when a kernel (black hole) is produced in the middle of an artifact body pair map, the risk of system divergence from the queueing theory increases as the input (demand) and output (supply) speeds converge. The risk of variations in the input and output may be avoided by providing a buffer (time) for demand matching. A stable (robust) operation of global artifact bodies is necessary to avoid the bankruptcy at managing of enterprise (artifacts) type, and this may be achieved by adjusting the demand versus supply mismatching with a look-ahead forward/feedback approach.

6. Conclusion and Outlook

The contribution of the paper is the findings of similarity and identification on nature (physics) vs. artifacts body, and the findings could be unified to the field of Newton’s Little formula, Matsui’s law, and Matsui’s ME at the pair map microcosm. Probably, this material might also be applicable and useful to a class of the twin systems (cycles) at the cyber (upper)-physical (lower) system.

This study began with a queueing matrix for the production of artifact bodies. Noting that our artificial society consists of input (demand), output (supply), and queueing/inventory systems, we devised pair maps as tools (strategic tables) for sublating the dilemma facing manufacturing integration (sales maximization versus cost minimization), starting with Matsui’s system as a basis for input and output. This has proven beneficial in providing a core basis for subsequent research and allowing for the fabrication of miniaturized models of artifact bodies to provide a microcosmic view.

Currently, inquiries have been made into artificial society. Microcosms of artifact bodies within this are miniaturized models consisting of 3M&I objects. These miniaturized models (from 3D to 2D) are considered as pair-map categories (created in 1983). The format (compass) of these pair maps has been found in corporate-producing entities and physical bodies in the natural world and economics; this format is expected to be verified and proven even further.

The observed underlying (deep) condensed structure (time model), and internalized (embedded) dynamism (fractal and wave motion equation), are numerically clarified from the expansion of these corporate-producing entity pair maps (Matsui’s theory). In addition, they also showed that the center of the pair-map hyperplane corresponded to a black hole (cone) in the universe, leading to a collapse of artifact bodies.

A nature-versus-artifact-body pair-body (OE) phenomenon is seen in (Matsui, 2016, 2018), and the pull-type in the merge process is believed to be a typical type of this ideal form. This type of ternary matrix (Maurus and Plant, 2014) is referred to as DAEn in Ternary SW, which resembles the Eastern danshari concept. DAEn bodies have duality matching and mismatching (skewness) problems in pair maps. A buffer based on proper delays (overflows) is expected to resolve this mismatching dilemma.

Thus, based on our research, a desirable measure (that does not reach a black hole) is a dual chameleon criterion (medium) according to input 1:output In2:buffer In2 in the upper part of a body (quantity/motion) with an efficiency of 0.6 versus a waste of 0.4 pull balancing in the lower part (money/energy system).

Finally, other than stochastic differential equations with numerical delays, Matsui’s ME type approaches may also be practical in the nature versus artifact world. We believe this will lead to the solutions found in classical analects, democracy, abacus, and debates on capital.

Acknowledgments
This paper is a translation into English of the following research paper, which has already been published in Japanese .Matsui, M., (2021) Bodies Science, Hyperboloid type and Nested Economics Sollen, Central Dualism and Chameleon’s Criteria in Nature vs. Artifacts Body (II), The 9th OHKAN Conference of NPO: Transdisciplinary Federation of Science and Technology, Tsukuba University, Japan.

References
Ashby, W. R. (1956). An introduction to cybernetics. London: Chapman and Hall Ltd.

Ashby, W. R. (1960). Design for a brain. London: Chapman and Hall Ltd.

Bittanti, S. A., Laub, J., and Willems, J.C. (1991). The Riccati equation: Springer-Verlag,

Matsui M., and N. Ishii. (2019). A demand-to-supply enterprise robot and its ODICS II type for convenience store application, Procedia Manufacturing, 39, 381–388.

Matsui, M., (2005). A management cycle model: Switching control under lot processing and time span,” Journal of Japan Industrial Management Association, 56(4), 256–264.

Matsui, M., (2002). A management game model: Economic traffic, leadtime and pricing settings. Journal of Japan Industrial Management Association, 53(1), 1–9.

Matsui, M., (2005). CSPS Model: Look-ahead controls and physics. International Journal of Production Research, 43 (10), 2001–2015.

Matsui, M., (2009). Manufacturing and service enterprise with risks: a stochastic management approach. Boston: Springer-Verlag.

Matsui, M., (2011). An outline on Matsui’s equation and its circumference. Bulletin of Kanagawa University, Research Institute for Engineering, 34, 2–5.

Matsui, M., (2013). A Chameleon criteria and medium control in efficiency versus Muda world. Bulletin of Kanagawa University, Research Institute for Engineering, 36, 40–45.

Matsui, M., (2013). An enterprise-aided theory and logic for real-time management.  International Journal of Production Research, 51(23–24), 7308–7312.

Matsui, M., (2016). Fundamentals and principles of artifacts science: 3M&I-Body System. Singapore: Springer Briefs in Business, Springer.

Matsui, M., (2018). Theory, formulation and realization of artifacts science: 3M&I-Body System: Springer Briefs in Business, Springer.

Matsui, M., (2020). A chameleon’s harmonic correlation, criteria, and diversity for a win-win and sharing world. Theoretical Economics Letters, 10, 735–744.

Matsui, M., and Fujikawa, H. (2005). Selling and manufacturing can collaborate profitably: Profit maximization theory of platemaking collaboration, clarifying a ‘pair strategy chart. Diamond Harvard Business Review, 30(1), 2–13.

Matsui, M., Ohto-Fujita, E. and Ishii, N. (2021). Humanized robot of new method & time system and its management: A digital transformation case of convenience store type. In Proceeding of 26th Int. Conf. Prod. Res., Taiwan.  

Matsui, M., Shingu, T. and Makabe, H. (1978). An analysis of conveyor-serviced production station by queueing theory. Journal of Japan Industrial Management Association, 28(4), 375–386.

Maurus S., and Plant, C. (2014). Ternary matrix factorization. In Proceeding of 2014 IEEE Int. Conf. Data Mining, pp. 400–409.

Nof, S., J. Ceroni, W. Jeong, and M. Moghaddam. (2015). Revolutionizing collaboration through e-work, e-business, and e-service. Springer ACES series, Springer,

Reis, L.L., J.J. Brennan, R. M. Crisp, Jr. (1967), A Markovian analysis for a delay of conveyor-serviced production station. International Journal of Production Research, 5, 201–211.

Walker, J. (2001). Principles of Physics. 9th. Ed: International Student Version, John Wiley.

Wiener, N. (1961). Cybernetics. Massachusetts: MIT press.

Yamamoto, H., Matsui, M, and Liu, J. (2006). Basic study on a limit-cycle problem with multi periods and optimal assignment problem,” Journal of Japan Industrial Management Association, 57(1), 23–31.