1. Introduction

Since Wiener’s cybernetics (Wiener, 1961), there is the Nature versus artifact science.  In there, the similarity and harmonic gap of nature of nature versus artifacy body are questioning, and the trap of similarity is seen at between human and biology classes.

Our study of a new field of academia (Matsui 2020a,2021) is now concluding, and has advanced from factory science (Matsui 2008, 2014b), economic bodies, natural versus artifact body science (Matsui 2016, 2019) to the embodiment of what they should be, and to calling for an artifact science (Matsui, 2021). Artifact science has moved a step further, and in the coronavirus pandemic, society has been confronted with the nano-world of viruses.

Digital society appears on the verge of transformation and being made smarter by quantum technology, but conventional discussions are diverged thinking and would be anxious to might be not unified at totality.

As to artifact science in this nano world, from the contrast between the quantum, the wellspring of matter, and the nano of 3M&I artificial bodies, I think the search will leap ahead to quantum science vs 3M&I science (the world of the nano-age). The natural nanoworld and intangible, artificial society are both situated in the world of state space in my theory of a paired hierarchy of artifacts, and could be considered invisible classes.

Even in the imaginary worlds we create, in comics, dramas, movies etc, we often see depictions of an unreal, non-ordinary, cyber world that transcends human beings. Games too; we are advancing from sports into games, and games are being viewed as real, embodied business. Today, approaches are being sought to this intangible nano-world and the nature of the knowledge society. The coming nano-world, together with the coronavirus pandemic, has seen the further questioning of what the ideal form of scientific natural vs artificial bodies should be, together with their design challenges. This form, its pair map microcosm and diversity are thought to mainly result from the duality of the quantity and money (value) system equations in Matsui’s Equation in the nano age, as with the duality of the motion and force (energy) equations in Newton’s law in quantum mechanics.

This binary of matching (cores) and misalignment (friction) manifest as various Nash’s zone phenomena in natural versus artificial bodies. In my previous papers (Matsui 2020b, 2020c), I discussed the ideal form of scientifically disconnected systems and the Nash’s zone (black hole) problem in the center of this natural versus artificial body pair map. In particular, the chameleon criteria for cores in this zone, their safety (robustness), and the manner in which they should be presented.

This paper proposes an outline of individual (body) microcosm by nature versus artifact science (Matsui 2014, 2016), and the field theory of its pair map microcosm and Nash’s zone (core) is developed. Finally, a case of nested economics is discussed toward win-win and sharing world.

First, it introduces a case where the core from my previous paper becomes a conic surfaces of an artifact, however separate papers (Matsui, 2020b; Matsui et al, 2021a) further expand on this, developing from a case where the core is considered to be a one-sheet (elliptic) hyperbolic surface. That is, this one-sheet (elliptic) hyperbolic surface is known to exhibit the ellipses, parabolas and hyperbolas shown on the pair map, depending on how it is sliced, and the general pair map shows the pair maps to date shaded in various ways using these three types of curves.

Next, it also proposes the fractal nesting hypothesis, which holds that the form of natural vs artificial bodies can generally be assumed to be one-sheet (elliptic) hyperbolic surfaces. The nested (core) model addresses the “thing type” like the human body and the “concept type” like social bodies, with the Nash’s zone problem considered to be at their core. In particular, various heterogeneity policies are given to ensure marginal diversity from the chameleon criterion in the core.

In the following sections, the generalized pair map reduction is given, Nash’s zone (core) hypothesis is presented at modern society and physics.  Finally, the economic trickle down theory would be discussed questionably.

2. Natural vs artificial bodies and what form they should take

2.1 An overview of the Individual pair map reduction method and one-leaf (elliptic) hyperbolic surface
The nature of natural versus artificial bodies and their design challenges are being questioned. This diversity of form is thought to mainly result from the duality of the quantity and money (value) system equations in Matsui’s Equation, like the duality of the motion and force (energy) equations in Newton’s law in quantum mechanics. This double matching and misalignment (friction) produces various natural versus artificial body phenomena.

From the paired matrix approach (Matsui 1983, 2005, 2014), a 3M&I body is regarded as a set of systems comprised of input-output systems (usually with goals), and these input-output systems have the function of maximizing output while minimizing input. We consider a binomial input-output matrix, termed a pair matrix, to be the input-output collaboration function for this purpose.

Each element of this matrix is a pair element (output gain, input loss). Various graphic patterns can be seen in the pair matrices of examples of natural and artificial bodies. Elliptic intersections are particularly characteristic, and in which elliptic rotation mechanisms can be seen, and are commonly termed pair maps as a generalization.

This intersecting ellipse has two intersecting axes linking manufacturing (input) and sales (output), one corresponding to positive correlation, termed “economy,” and the other to an inverse correlation, termed “reliability.” The intersection resulting from this tug-of-war is the goal of the body (profit maximization), and is an equilibrium balance point (Win-win or point of variation). A variant hyperbolic type can be found here, with its orbit toward the center.

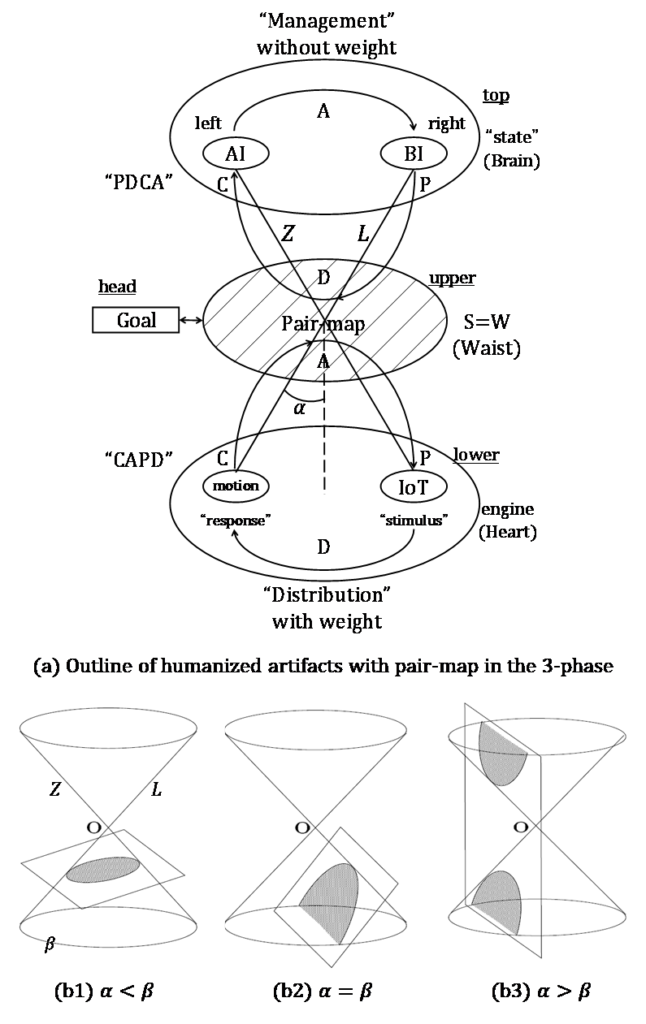
The form of natural vs artificial bodies is considered to be a one-leaf (elliptic) hyperbolic surface in Figure 1, susthis pair map is called “Nash’s zone,” within which nest cores. The nested surface is considered to be a one-leaf hyperbolic surface, and parabolas, ellipses and hyperbolas can be formed from various cross-sections. This top-down microcosm (microverse) can be represented as a pair map.as the three types.

A type of Sollen at nature versus artificial body was first visualized as humanized body at Matsui (2020) and Matsui et al (2021) in Fig.1(a), and could be now regarded as one-leaf hyperboloid at geometry. The three round slices in Fig.1(b) is generally known as the ellipse, parabola and hyperbola types, and the pair-map is likely to a prism of one-leaf hyperboloid.

At Fig.1, there is labelled the axis of economics, Z, and of reliability, L, seen at Fig.2, too. The Z and L is here introduced from Matsui’s equation (W=ZL) in 1977 (Matsui, 2020a) as the base of nature versus artifacts body. Note that, by Matsui’s equation, the cycle, Z, means the revenue (sales), the amount, L, means the assets or fund the lead-time, and the product, W, means the assets or fund.  

2.2 Generalized pair map reduction and Nash’s zone
The body pair map of natural vs artificial bodies is seen as a (α,β)-balance screen on the paired matrix surface at Fig.1, and has been refreshed to that shown in Figure 2, having developed from the initial pair map of elliptic intersections (Matsui 1983; Matsui et al 2005) to a developed version focusing on hyperbolic slices (Fig 1.). At fig.2, the (α,β)-balance of pair-map would vary by through “(b1)α<β―>(b2)α=β―>(b3)α>β”.

In Fig.2, the elliptical intersection of Economy (Z) and Reliability (Lbar) is balanced by the diversity/integration hyperboloid. The central region in particular is known as Nash’s zone. At first, the so-called Nash’s zone is already appeared at Appendix in Matsui (2019) as the barrier on the goal of artifact body. Recently, we ascertain the following equilibrium inequality:

Integration (Muda)  > Nash’s zone (Chameleon’s diversity)  < Sharing (efficiency)

by an Information Theory approach (Matsui, 2016). The Muda is a Japanese and means such as the delay, overflows, redundancy etc. as constraints in cybernetics.

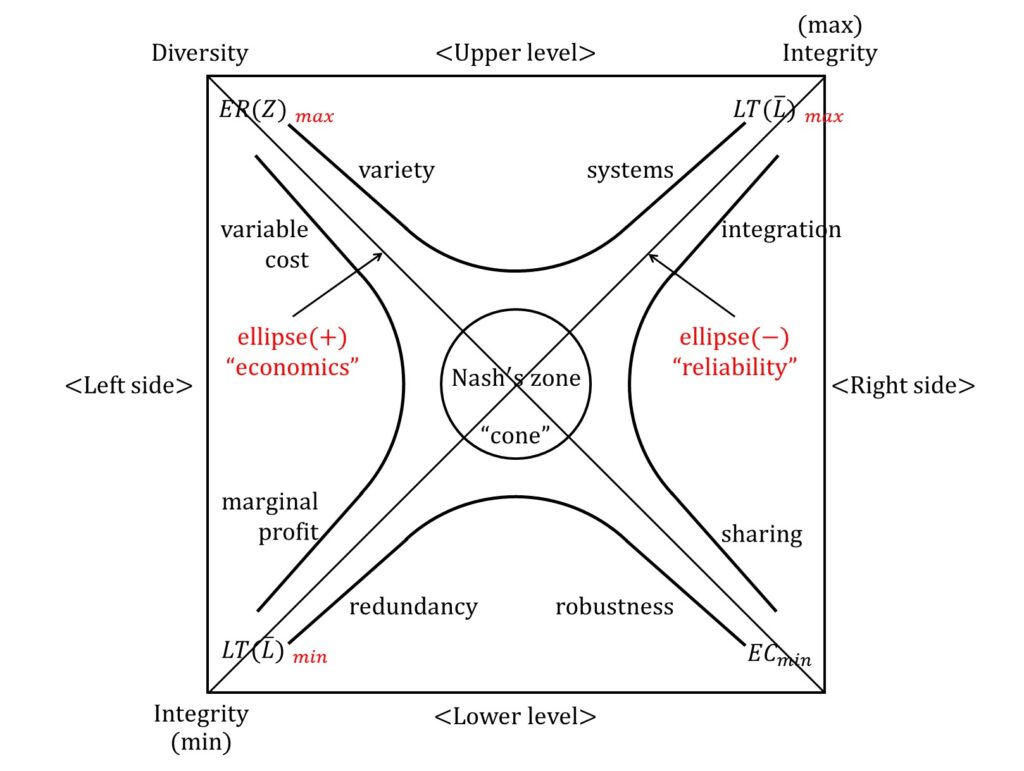
Second, the pair map is originated in Matsui (1983), and the cross-ellipse type (Z, L) at Fig.2 is developed and known at the three sales & manufacturing enterprise type (Matsui et al 2005; Matsui 2008). Recently, a pair of hyperbola, ZL, is added to the cross-ellipse in Fig.2 from Matsui (2020) and Matsui et al (2021), and the outline of generalized pair map is imaged and semi-finalized at Fig. 2. This would be similar to the nature body, for example, physics body seen at Matsui (2019).

3. Pair map reduction of natural vs artificial bodies

3.1 The Nash’s zone core hypothesis and nesting: Enterprise or society type

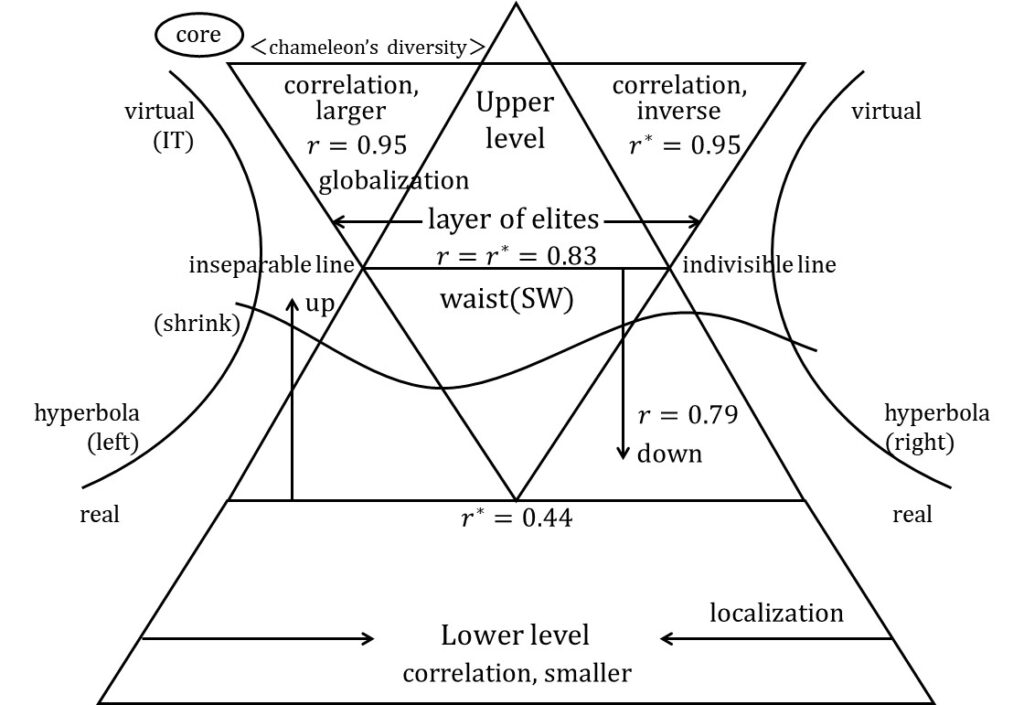
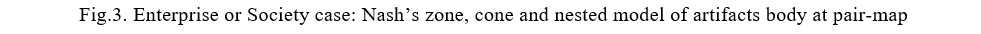
The Nash’s zone at the center of Fig.2 is the area of both marginal profit maximization and maximum gravity, but now we consider the core hypothesis as distinct from the existence of the kernel. This core is considered to be nested, with Figure 3 presenting a typical example. The bottom layer of the body is the visible, real world, while the invisible bottom layer is the virtual world. This mixed state requires a science offering a nano world-view.

Traditional cores are known as the so-called pyramid shape. However, this pyramid shape is recently separating at waist (bottle of middle level) by the educational disparity and increasing intelligentsia due to poverty. In fig.3, r is correlation coefficient, and r* is inverse correlation coefficient at the three examples of correlation table in Matsui, 2020). The so-called Nash’s zone is r=r*=o,83 at correlation, and Chameleon’s criteria (0.4) are correspond to the marginal diversity at economics (Matsui, 2020), and effective reproduction number at herd immunity theory (Matsui et al, 2021b).

3.2 The ideal for natural vs artificial bodies as seen through science

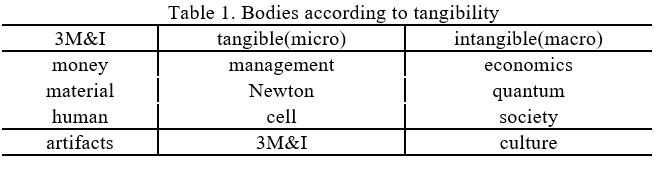
The ideal form for natural vs artificial bodies when viewed scientifically can be seen in Table 1 as an overall example of the world we live in, and these are connected in a nested manner, or something similar. Table 1 categorizes the forms of bodies in the world we live in by whether they are tangible or intangible. In Figure 4, we can see a general wireframe example of the nested cores of a body.

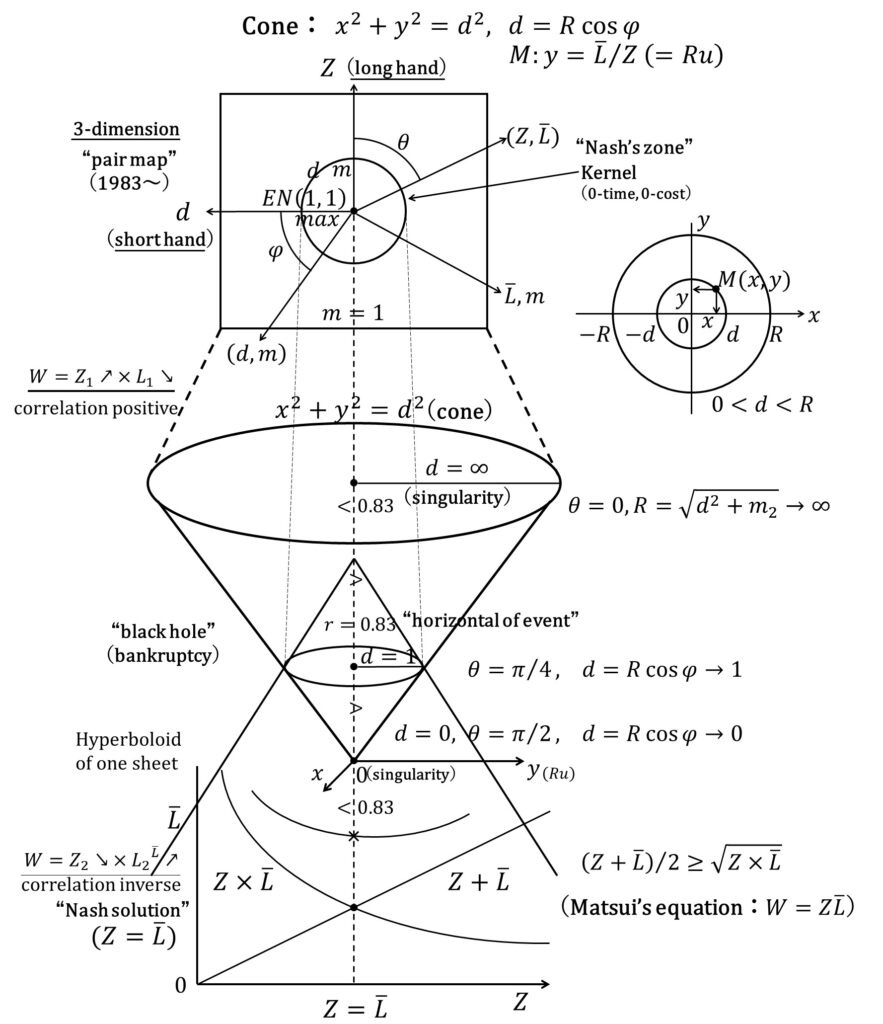
Also, Fig.4 shows the clock-typed dynamics of pair map. If the clock system consists of the short hand (Z) and long hand (Lbar), then physics body behaves at the wave equation. In addition, it is seen that its center has conical surface (Matsui, 2019) and would be similar to core. At the bottom of Fig.4, it is noted that the classic inequality on the Z and Lbar at pair map.

The upper part of Fig.4 shows a pair map, while the lower part shows the graph of the Nash solution (Z=Lbar). In the center, in the core (Nash’s zone) of this conical pair, we can see the corresponding one-leaf hyperbolic surface. Recent economic and democratic disparities have produced misalignment and distortion in the center, and there is a need to harmonize economic systems.

4. A Realization Case of Pair Map Microcosm

4.1 Nesting ordered systems and the Trickle-Down Problem

Generally, the so-called trickle-down theory at economics has been contributed to the functioning income distribution, but I wonder if this functioning is scientifically fair. For the problem, we could here utilize our pair map microcosm, and would like to show a new finding by a theory of ordered entry system (Matsui et al, 1977).

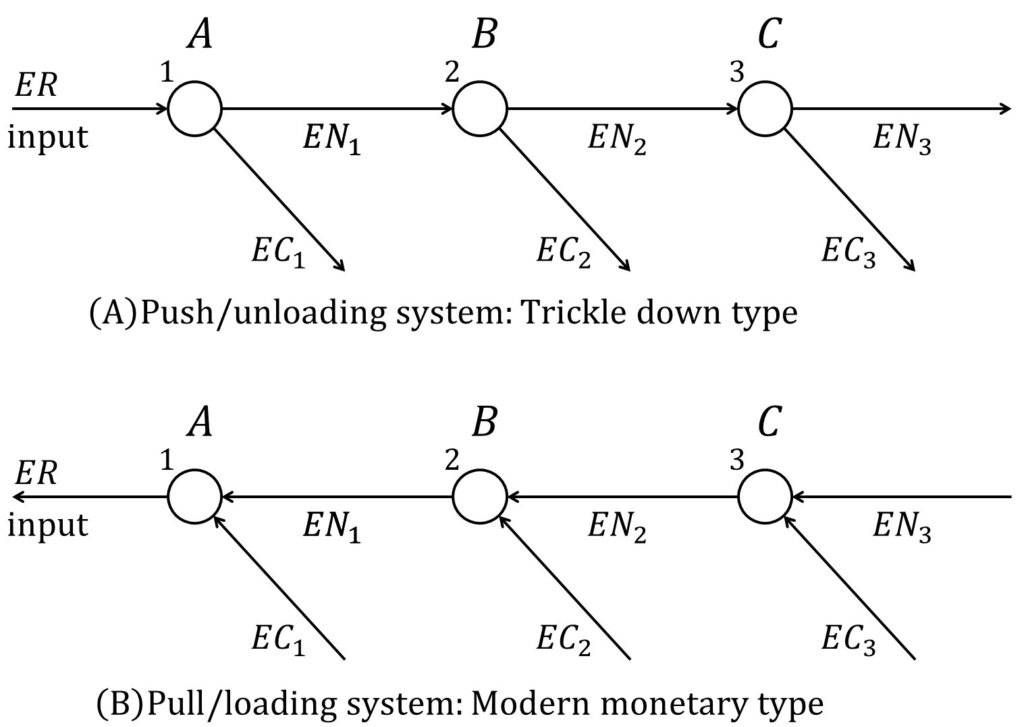
That is, the overlap of economic nesting can be seen in supply, demand and inventory systems when we consider ordered flows. Figure 5, for example, shows a push (trickle-down) system, and a pull (modern monetary theory, MMT) system. In the former, an increase in base money means (pushes) lending by banks in mainstream economics, while in the latter, in modern monetary theory, increased bank lending means (pulls) increased base money.

From the standpoint of bodies sharing equilibrium in our ordered nested model, this problem can be ameliorated by applying Win-win & sharing theory to this trickle-down system, and the Share up-income & down-expense hypothesis is proposed as the ideal form of the economic body. This is the minimization-oriented theory of overflow from the top (Nash’s zone), and it is thought that deeper balancing will be promoted under modern monetary theory.

4.2 Bodies’ shared equilibrium and an example of Win-win & sharing
Considering the core (income category) nesting model for economic bodies, this can be viewed as a lot Q manufacturing problem. Where the lot size is less than or equal to 1, an archetype can be found in the ordered Entry (OE) flow system where income (earnings) is the input. This can be regarded as equivalent to the nested B = X, Y, Z flow system ordering problem (LPT rule), which resembles recent trickle-down theory.

The shared balancing solution for income bodies in lot Q<1 is a form of Nash solution ( c), with a lost-call rate of . Now, in the push system (unloading), we obtain the following formulation (1), (2) as a shared equilibrium problem (Matsui 2018, 2019). Foresight (look-ahead) vector  is accompanied by the ordering of income in increasing order (LPT rule), and results from monotonicity (decreasing order).

Vector in evaluation equation (1) is a kind of time buffer, which in this case means the range on the physical line. Moreover, the constraint equation (2) is an average constraint equation of the Matsui’s equation type, and relates to the equivalence of the sharing <vertical plane> and balancing <horizontal plane>. This is the shared balancing condition.

Here, taking the flow rate to be , the optimization (equilibrium) condition is given by the following equation:

Then, it is desirable to set: Thus, from Equation (3), series , and can be obtained sequentially as follows:

By following the equation (4), Fig.6 is derived and utilized from a discussion example (Fig.2.12, Matsui 2018) at the win-win and sharing society. At Fig.6, the objective is (A)25.2 + (B)5.44 = 30.64 (sharing), and is not fair and smaller at income distribution.

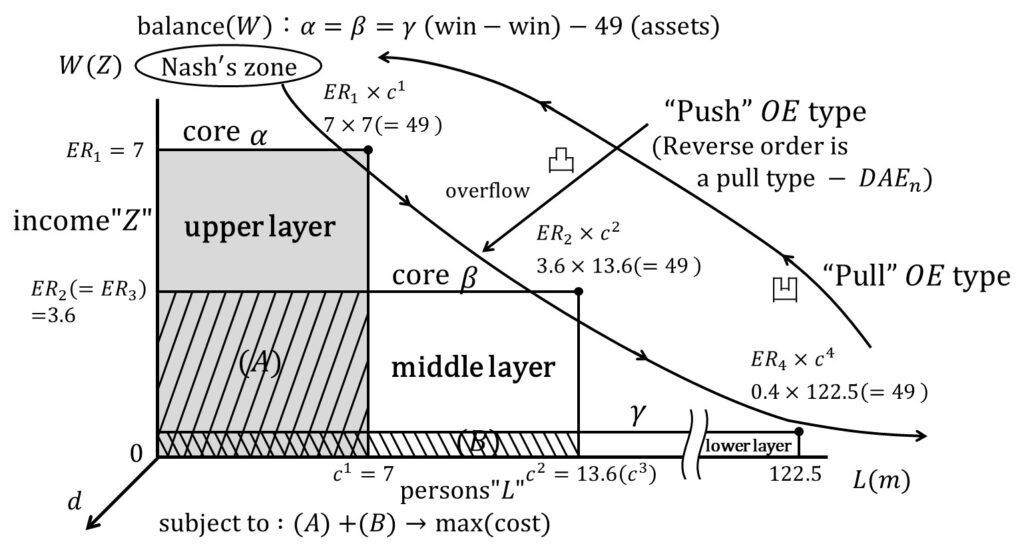
In the pull-type (loading), the money flow is Z -> Y -> X (Fig.5(b)), and flows uphill toward Nash’s zone: and it is found that the overall utilization rate improves in the production system where the processing speed is in reverse order (slowest to fastest) (Matsui et al, 1977). Considering the order of income, if the first is gradual, the middle quick and the last up, the overall income level can be expected to improve. This is the share up&down concept in this paper, and provides a table of the ideal form of economic and social discussion

5. Conclusion and the future

Drawing the perennial exploration of pair maps since around 1983, this paper presents an outline of natural vs artificial bodies in its depths, which is a one-leaf (elliptic) hyperbolic surface. The root of this bodies science is the quantum and cell of the nano world, corresponding to the 3M&I of artificial bodies. The three have a shared mechanism, the clock system (paired duality), and the integrated system composed of these three is an entire fractal.

The form of the body is considered to be nested as seen in the pair maps and various three-dimensional microcosms. This is characterized by a cross-sectional ellipse or hyperbola at the sliced end, and the cores are termed Nash’s zones (kernel). When viewed in three dimensions, the body map is shaped like Mt. Fuji, with the center (summit) likely corresponding to the volcanic crater.

The movement of the body is considered to be a dynamic up&down action in the field centering on the raised summit. This is thought to be similar to recent developments in economics and trickle-down theory, and these have been linked to it. From the standpoint of the ordered nested model, the Win-win & sharing theory can be applied to this trickle-down problem, and the Share up&down hypothesis is proposed as the ideal state of the economic body.

This is an area of theory oriented towards minimizing overflow from the top. Further exploration of this type of body science offering a nano world-view is desirable going forward; bodies are in a state in which visible real space and invisible virtual space are mixed, and we seem to be moving toward a field of science in which the need to visualize and reproduce the new invisible world will be queried.

Finally, it is noted that the possibility of the study would be depend to the presence or absence of goal itself at nature versus artifact body.

Acknowledgments
This paper is a translation into English of the following research paper, which has already been published in Japanese. Matsui, M., (2021) Bodies Science, Hyperboloid type and Nested Economics
Sollen, Central Dualism and Chameleon’s Criteria in Nature vs. Artifacts Body (II), The 9th OHKAN Conference of NPO: Transdisciplinary Federation of Science and Technology, Tsukuba University, Japan

References
Matsui, M. (1983), A Game Theory-based Study of Order Selection and Capability Switching Measures, Preprints for the Fall Meeting of the Japan Industrial Management Association, Hiroshima University, 48-49.

Matsui, M. (2008), Manufacturing and Service Enterprise with Risks: A Stochastic Management Approach, International Series in OR&MS, ISOR125, Springer

Matsui, M. (2014a), Study on IO matrix systems: The generalization of pair matrices and the pair matrix expansion problem, The 5^th Transdisciplinary Federation Conference, University of Tokyo Faculty of Engineering, November [In Japanese]

Matsui, M. (2014b), Manufacturing and Service Enterprise with Risks II: The Physics and Economics of Management, International Series in OR&MS, ISOR202, Springer, 2014.

Matsui, M. (2016), Fundamentals and Principles of Artifacts Science: 3M&I-Body System, Springer Briefs in Business, Springer

Matsui, M. (2018), A Theory of Modern Economic Growth toward Sharing Society, Theoretical Economics Letters, 8, 675-684.

Matsui, M. (2019), Theory, Formulation and Realization of Artifacts Science: 3M&I-Body System, Springer Briefs in Business, Springer

Matsui, M. (2020a), A New Academic Discipline: Advancing Factory Science, Economics and Artifacts Science, Research Outreach―Connecting Science with Society, (114) 82-85.

Matsui, M. (2020b), A Chameleon’s Harmonic Correlation, Criteria, and Diversity for a Win-Win and Sharing World, Theoretical Economics Letters, 10, 735-744.

Matsui, M. (2020c), What natural vs artificial bodies should be, Central duality and the Chameleon criterion, The 11^th Transdisciplinary Federation Conference, October, The Institute of Statistical Mathematics [In Japanese]

Matsui, M. (2021), My management engineering, the path to the study of learning and undiscovered thought, Communications of Japan Industrial Management Association, 30(2), 93-97 [In Japanese]

Matsui, M., Fukuta, J. (1977), On a Multichannel Queueing System with Ordered Entry and Heterogeneous

Servers, AIIE Transactions, 9(2), 209-214.

Matsui, M., Fujikawa, H. (2005), “Pair Strategy Charts” reveal the profit maximization theory of manufacturing-sales collaboration,” DIAMOND Harvard Business Review, 30 (1), 2-13. [In Japanese]

Matsui, M., Ohto-Fujita, E., Ishii, N. (2021a), Humanized robot of New Method &Time System and its Management:

A Digital Transformation Case of Convenience Store Type, Proceedings of 26^th International Conference on Production Research, Taiwan, July

Matsui, M., Ohto-Fujita, E., Ishii, N. (2021b), A Humanized vs. Managerial Body System of H (heart) = W (waist) = L (lung) Type by Nature vs. Artifacts Science, Preprints for the Spring meeting of Japan Industrial Management Association, Waseda University, Tokyo

Wiener, N. (1961), Cybernetics, MIT press, Massachusetts